Скорость — это физическая величина, характеризующая быстроту изменения положения объекта относительно времени. Она измеряется как отношение пройденного расстояния к интервалу времени, за который это расстояние было пройдено.
Скорость может быть постоянной или изменяться со временем, и в зависимости от этого различают равномерное и неравномерное движение. В качестве единицы измерения скорости в системе SI используется метр в секунду (м/с), но также могут применяться и другие единицы, такие как километры в час (км/ч) или миллиметры в минуту (мм/мин).
Кинематика
Мир полон движения. Мы часто говорим, что прошли какое-то количество километров, оплачиваем штрафы за превышение скорости и выбираем самый быстрый маршрут в навигаторе. В этой статье научимся решать основную задачу механики — определять положение тел в данный момент времени.
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
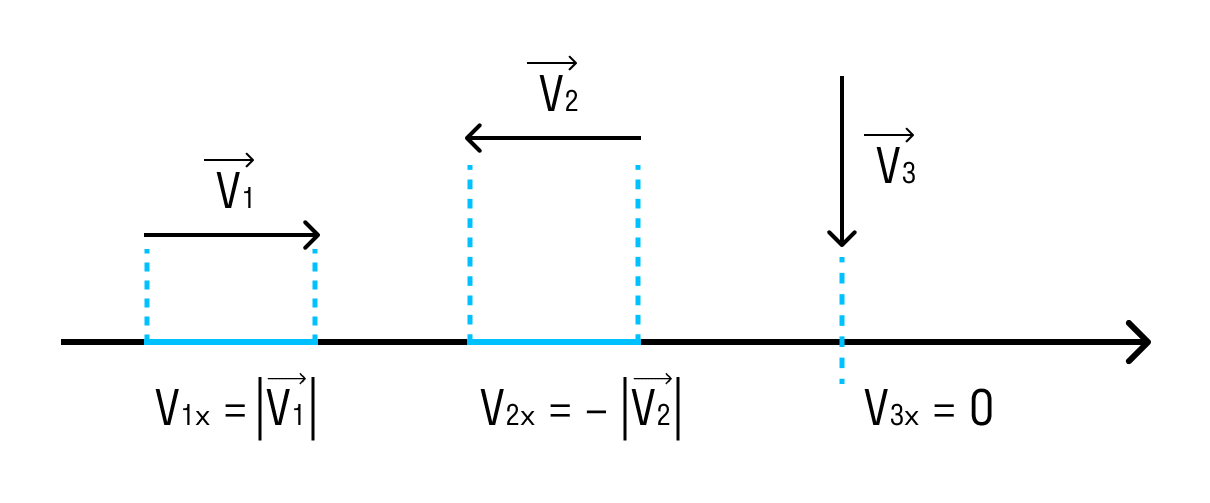
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с] — перемещение [м] — время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
V ср.путевая = 210/2,5 = 84 км/ч
автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м] x0 — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м] x0 — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с]

Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
То есть равноускоренное прямолинейное движение — это движение с ускорением по прямой линии, движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
x(t) — искомая координата в момент времени t [м] x0 — начальная координата [м] v0x — начальная скорость тела в [м/с] t — время [с] ax — ускорение [м/с 2 ]
Для данного процесса Важно уметь находить конечную скорость. Это часто упрощает решение задач. Она находится по формуле
Формула конечной скорости
— конечная скорость тела [м/с] — начальная скорость тела [м/с] — время [с] — ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения: a = v/t = 60/0,05 = 1200 км/ч 2 Теперь возьмем уравнение движения. x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки: км
через полчаса координата автобуса будет равна 150 км.

Какая профессия тебе подходит? Узнай за 10 минут!
Получи больше пользы от Skysmart:
- Подтяни оценки на курсах по физике.
- Выбирай из 890+ репетиторов по физике.
- Записывайся на бесплатные курсы для детей.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки. Очень важно разделить движение по окружности и вращение тела.
При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.
При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.
Центростремительное ускорение
При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.
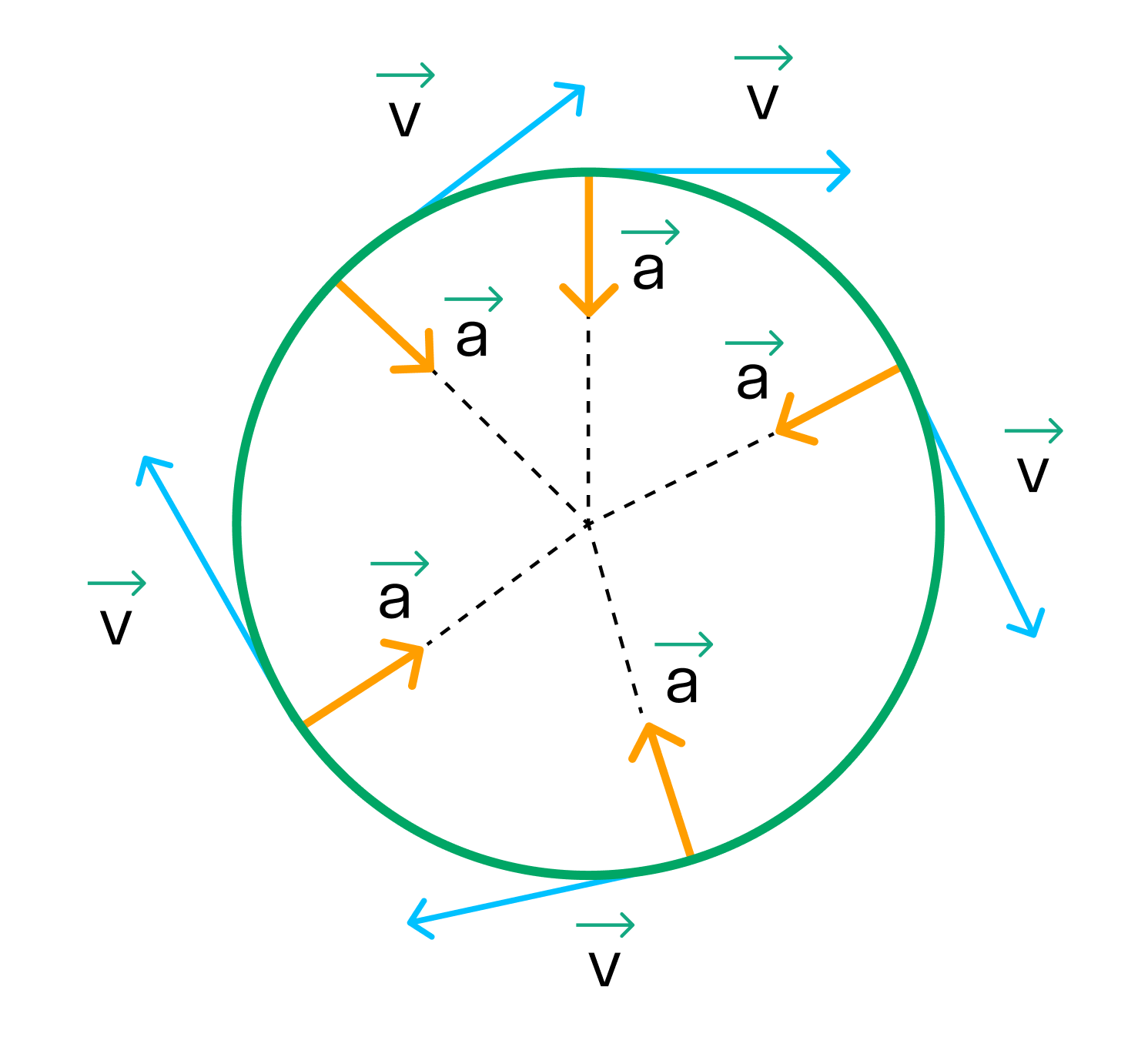
Центростремительное ускорение
aц = v 2 /R
aц — центростремительное ускорение [м/с 2 ]
R — радиус окружности [м]
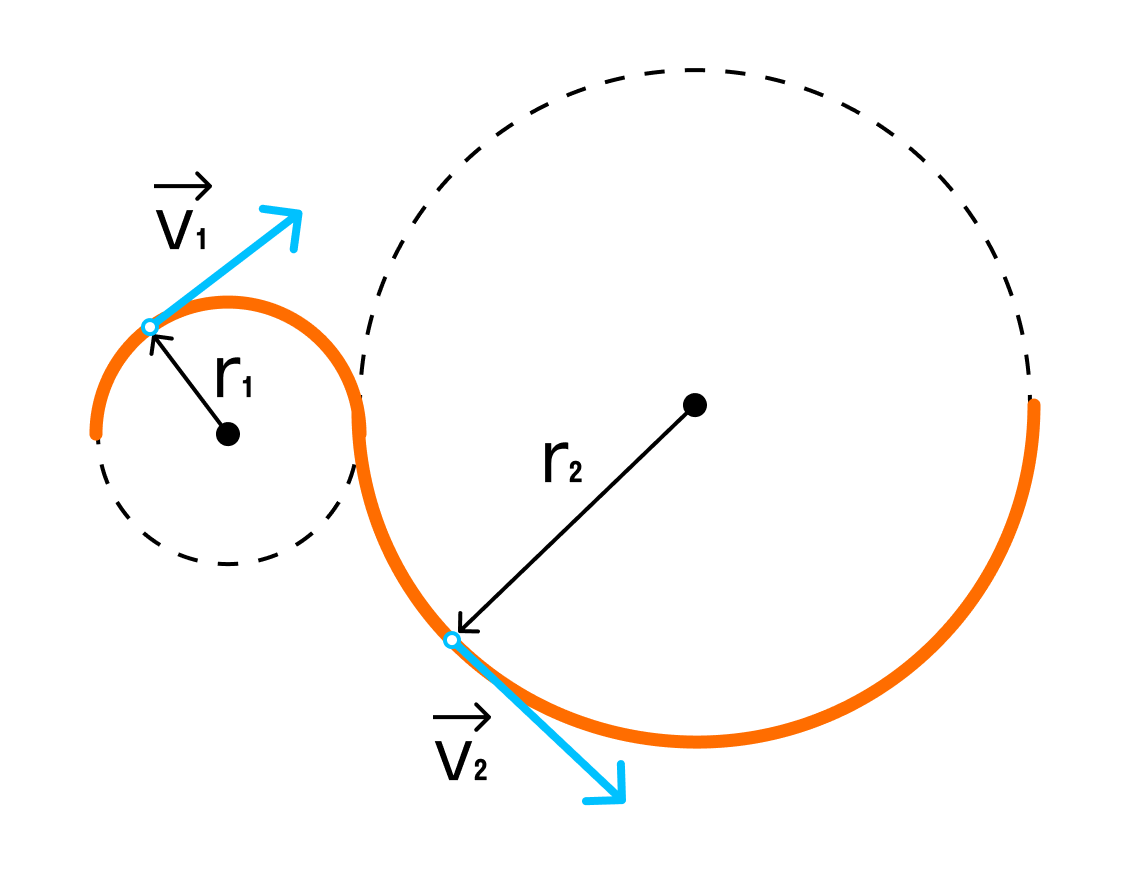
Задачка
Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?
Решение:
Возьмем формулу центростремительного ускорения тела
В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.
Теперь можно подставить значения в формулу:
aц = 10 2 /120 = 100/120 = 10/12 ≃ 0,83 м/с 2
центростремительное ускорение мотоциклиста равно 0,83 м/с 2
Эту и другие темы мы разбираем на курсе физики за 9 класс.
Определение скорости. Школьный курс физики

Скорoсть — понятие, с которым мы вначале сталкиваемся в реальной жизни, затем встречаем на математике и только затем изучаем в курсе школьной физики. Попробуем разобраться с физическим смыслом этой величины с использованием простых примеров.
Физический смысл и определение скорости

Понятие «скорость» встречается ученикам не только в школьном курсе физики за 7 класс. Гораздо раньше дети знакомятся с ним в реальной жизни, на интуитивном уровне понимая значение «быстро» или «медленно». Мы достаточно рано узнаем, что автомобиль едет быстро, а улитка ползет медленно. Ракета летит еще быстрее автомобиля, а время — то летит, то тянется.
Ситуация становится еще запутаннее, если мы посмотрим на кухню, где готовится какое-то блюдо. Если оно любимое — то готовится долго, а съедается быстро. Если нелюбимое — тогда наоборот. Или каникулы или выходные — они всегда проходят с феерической скоростью, а вот учебные дни всегда тянутся медленно.
Неудивительно, что в физике понятие «скopость» также используют часто и для разных применений. Есть скорость движения объекта (даже и не одна), протекания химических реакций (вы уже познакомились с ними в курсе химии), изменения температуры. Фактически это быстрота (вы удивитесь, но в физике есть термин «быстрота») какого-либо действия.
Система отсчета

Разберем значение системы отсчета, поскольку она имеет огромное значение для изменения скорoсти. Это тоже физическое/математическое понятие, и весьма сложное, которое будет изучаться позже. Сейчас нам достаточно понимать, что скорость можно измерять в привязке к какому-то объекту. Пример.Представим себе движущийся поезд с абсолютно прозрачным корпусом. Удобно, ведь стоя возле железной дороги, мы можем наблюдать за жизнью пассажиров. Сейчас такой поезд пролетает мимо на скорости 300 километров в час, но мы успеваем заметить, что ребенок бросил мячик на пол — и этот мячик катится по полу и с нашей точки зрения делает это очень быстро.Даже обгоняет поезд — то есть скорoсть мячика превышает 300 км/ч. Впечатляет. В то же время для ребенка, бросившего игрушку, ее скорость невелика — около 2-3 километров в час.И вот мячик прекратил движение. С точки зрения ребенка его скорость равна 0 км/ч, но с нашей точки зрения объект четь замедлился, но все еще движется со cкоростью поезда, то есть 300 км/ч.Вывод: Скорость каким-то образом зависит от точки зрения наблюдателя, то есть от выбранной системы отсчета.Рассматривая этот пример, мы намеренно ввели одну из единиц измерения скорости движения — километры в час (км/ч). Это очень наглядное обозначение, где в числителе у нас единица длины, а в знаменателе — единица времени. Есть и другие единицы измерения:
- метры в секунду или м/с (в системе СИ), например, скорость звука в воздухе составляет около 331 м/с;
- км/с — удобно использовать для очень быстрых объектов, например, скорость света составляет около 300 тыс. км/с;
- другие величины, например сантиметр в секунду или см/с (улитка движется со скоростью около 6 см/с).
То есть скорость равна расстоянию, которое объект проходит за определенный отрезок времени. Но не все так просто.
Что не так со скоростью
Представим себе, что автомобиль движется между населенными пунктами с промежуточными остановками.
Расстояние между ними составляет 60 километров, которое транспорт преодолевает за 1 час, следовательно, скорость на всем маршруте составит 60 км/ч. Вместе с тем половину пути, 30 км, машина преодолела за 15 минут или за 0,25 часа, то есть его скорость на этом отрезке была:
Так какая же скорость правильная, 60 или 120 км/ч?
В школьном курсе физике самое первое знакомство со скоростью происходит при условии равномерного прямолинейного движения.
Каковы же особенности этого движения:
- равномерное — в любой интервал времени объект преодолевает одинаковое расстояние (автомобиль из примера двигался иначе);
- прямолинейное — движение осуществляется вдоль прямой линии (вероятнее всего, машина также двигалась не по прямой, хотя бы из учета кривизны Земли и поворотов на трассе).
В реальной жизни равномерное прямолинейное движение если и встречается, то нечасто. Мы сами и все движущиеся объекты, ускоряются и замедляются, а то и стоят на месте (со скоростью 0 м/с), изменяют направление.
Но для простоты расчетов и для введения во «Вселенную скoрости» этого будет достаточно.

Катер движется по реке равномерно и прямолинейно со скоростью 60 км/ч. Определить, за какое время он преодолеет расстояние в 30 км.
У нас есть базовая формула, которая связывает время, перемещение и скорость:
Выразив из нее время, получим:
0,5 часа или 30 минут.
Скорость. Единицы скорости
За одно и то же время различные тела могут проходить разные расстояния. За 5 мин движения поезд прошёл большее расстояние, чем проехал велосипедист, а велосипедист большее расстояние, чем пролетела муха. Значит, одно и то же расстояние поезд проезжает быстрее, чем велосипедист, а велосипедист быстрее, чем пролетает муха.

ПОНЯТИЕ СКОРОСТИ
В физике быстроту перемещения тола характеризует такая величина, как скорость. Например, человек может за время 1 ч пройти путь 5 км, автомобиль за это же время может проехать 60 км, а самолёт пролетит 850 км. Тогда говорят, что человек движется со скоростью 5 километров в час, скорость автомобиля составляет 60 километров в час, а скорость самолёта — 850 километров в час.
В окружающем нас мире встречаются самые разные скорости. Так, черепаха может ползти со скоростью от 0,05 до 0,14 м/с. Идущий в среднем темпе человек движется со скоростью 1,4 м/с. Скорость гепарда может превышать 30 м/с. Скорость ветра во время урагана может превышать 32,6 м/с.
Звук в воздухе распространяется со скоростью приблизительно 333 м/с. а Земля движется вокруг Солнца со скоростью около 30 000 м/с. Скорость света в вакууме — самая большая скорость во Вселенной равна 299 792 458 м/с.
СКОРОСТЬ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ
Скорость при равномерном движении тела показывает, какой путь проходит тело за единицу времени. Так как при равномерном движении тело за равные промежутки времени проходит равные пути, то скорость при таком движении оказывается постоянной.
Для того чтобы определить скорость тела при равномерном движении, необходимо путь, пройденный телом, разделить на время, за которое этот путь пройден.
Если обозначить величины: скорость ʋ, путь — s и время — t, то скорость рассчитывают по формуле ʋ = s / t.
ЕДИНИЦЫ СКОРОСТИ
В Международной системе единиц (СИ) за единицу скорости принимают скорость такого равномерного движения, при котором движущееся тело за 1 секунду проходит путь, равный 1 метру. Эту единицу называют 1 метр в секунду и обозначают 1 м/с.
Очень часто используются и другие единицы скорости: километр в час (км/ч), километр в секунду (км/с), сантиметр в секунду (см/с). При выборе разных единиц скорость тоже будет иметь разные численные значения.
НАПРАВЛЕНИЕ СКОРОСТИ
Величины, которые, кроме числового значения (модуля), имеют ещё и направление, называют векторными. Числовое значение векторной величины также называется модулем вектора

Скорость, кроме числового значения, всегда имеет направление, следовательно, скорость — это векторная величина. Именно поэтому скорость обозначается как (со стрелочкой), а её модуль как ʋ (без стрелочки).
Говоря о модуле скорости, мы можем понять, насколько быстро или медленно движется физическое тело. Для решения большинства задач необходимо ещё знать, куда направлена скорость тела.
Кроме скорости, существуют и другие векторные физические величины, которые характеризуются числовым значением и направлением (с ними вы познакомитесь чуть позже). Вместе с тем существуют и другие физические величины, которые не имеют направления, а характеризуются только числовым значением. Такие физические величины называют скалярными. Примерами скалярных величин могут служить путь, объём, площадь и т. д.
ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ
Путь, пройденный телом, и скорость его движения с течением времени могут изменяться. Для большей наглядности эти изменения часто изображают графически.
Для построения графиков на горизонтальной оси (абсцисс) откладывают время, а на вертикальной оси (ординат) — путь, пройденный телом, или его скорость.
График зависимости скорости от времени при равномерном движении — это прямая, параллельная оси абсцисс. Действительно, с течением времени скорость при таком движении остаётся постоянной.
График зависимости пути, пройденного телом, от времени при прямолинейном равномерном движении — это прямая, расположенная в первой четверти координатной плоскости и проведённая из начала координат. Действительно, при движении тела с постоянной скоростью с течением времени путь, пройденный телом, увеличивается. Причём эта зависимость прямая, так как она описывается уравнением s = ʋt.
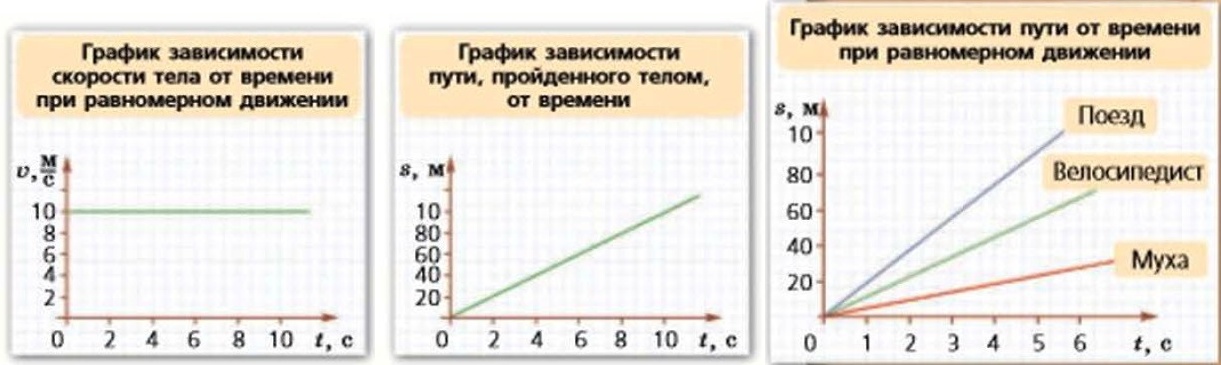
Вы смотрели Конспект по физике для 7 класса «Скорость»: Что такое скорость. Как можно определить скорость движения тел. Каковы единицы скорости. Как вычислить скорость тела при равномерном движении. Как построить графики зависимости скорости от времени.
Как построить графики зависимости пути от времени.




